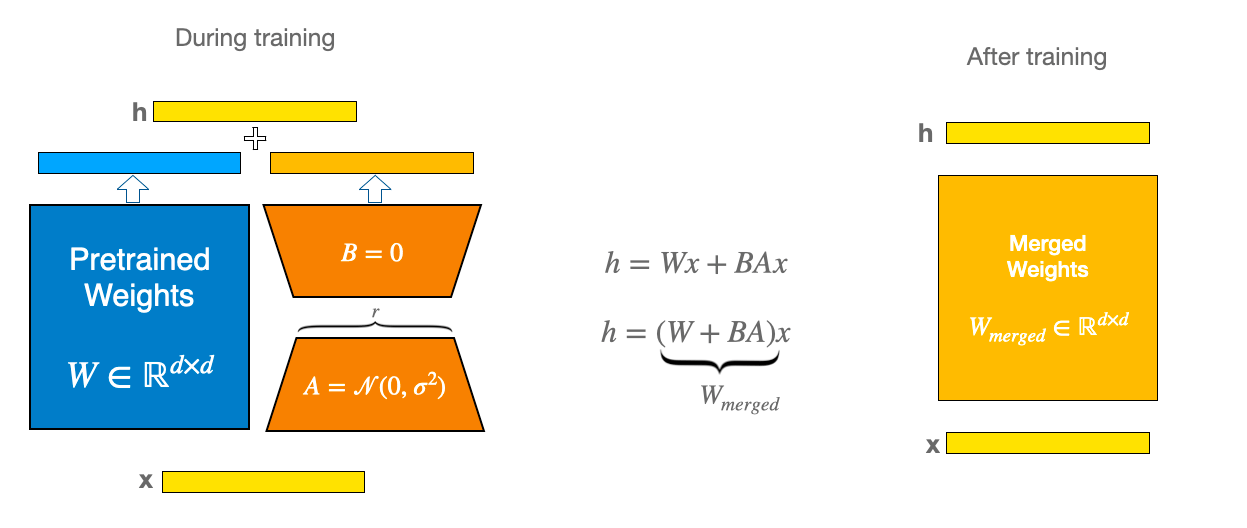QLoRA Explained: Fine-Tuning Large Language Models

In the age of Large Language Models (LLMs), we are witnessing two concurrent trends: the emergence of massive, general-purpose models such as LLaMA, Mistral, and Falcon, alongside the rise of highly specialized, efficient SLMs like Phi-2, GPT-Neo, and DistilBERT. These developments, reminiscent of Moore’s Law, underscore the rapid transformation occurring in the world of AI. As models become more ubiquitous, the fundamental question evolves. It’s no longer just about how things work, but about how they can work efficiently. And this shift is unraveling a whole new set of questions.

The Quest for Efficiency

In order for our AI economy to take off, we cannot have multi-year waitlists for chips. Necessity is the mother of invention. And so we have to be able to do more with less.

In this quest for efficiency, especially in the realm of fine-tuning, a standout technique emerges: QLoRA (Quantized Low-Rank Adaptation)…This is what we will chat about today.

Now if I put my faith in magic, I might not make the best engineer. That said, upon first encountering QLoRA, it’s hard not to feel like you’ve stumbled upon a bit of sorcery….

So you’re telling me you can drastically reduce the precision of your model and still achieve near identical model performance? Huh?

Yes! The essence of QLoRA's "magic" lies in its trade-off: it employs low-precision storage, significantly reducing GPU memory usage, while ensuring high-precision computations for optimal performance. This balance between storage efficiency and computational accuracy is what sets QLoRA apart in the realm of fine-tuning techniques.

Before diving deeper, let’s clarify: QLoRA combines LoRA's strategy of selectively tuning model parameters with advanced quantization techniques, splitting its innovation into two main components. The first is the LoRA technique itself, which focuses on parameter efficiency, and the second is the application of quantization, which involves various methods to optimize storage without compromising the model's effectiveness. We will explore each of these aspects in an intuitive manner, laying the groundwork for a deeper understanding of QLoRA.

Fine-Tuning

So first, what even is fine-tuning? Let’s understand via an example. I’m a sucker for some good Indian food. Imagine craving authentic Indian cuisine, but your AI, Llama, only offers generic, bland recipes. Not satisfying, right?

By feeding Llama-13b a specialized diet of hundreds of Indian recipes, we transform it from a generalist into Llama-13ji, an AI specifically adapted to master the art of Indian cuisine.

Jokes aside, this is fine-tuning in a nutshell: taking a broad-skilled AI and honing its expertise with a dash of specialized data, turning it from a jack-of-all-trades into a master of one.

Parameter Efficient Fine-Tuning (PeFT) & LoRA

Contrary to full fine-tuning, which adjusts all model weights, Parameter Efficient Fine-Tuning (PeFT) encompasses a variety of techniques designed to adjust a small subset (typically <1-5%) of a model's parameters. This approach not only conserves GPU and CPU resources but also simplifies the fine-tuning process.

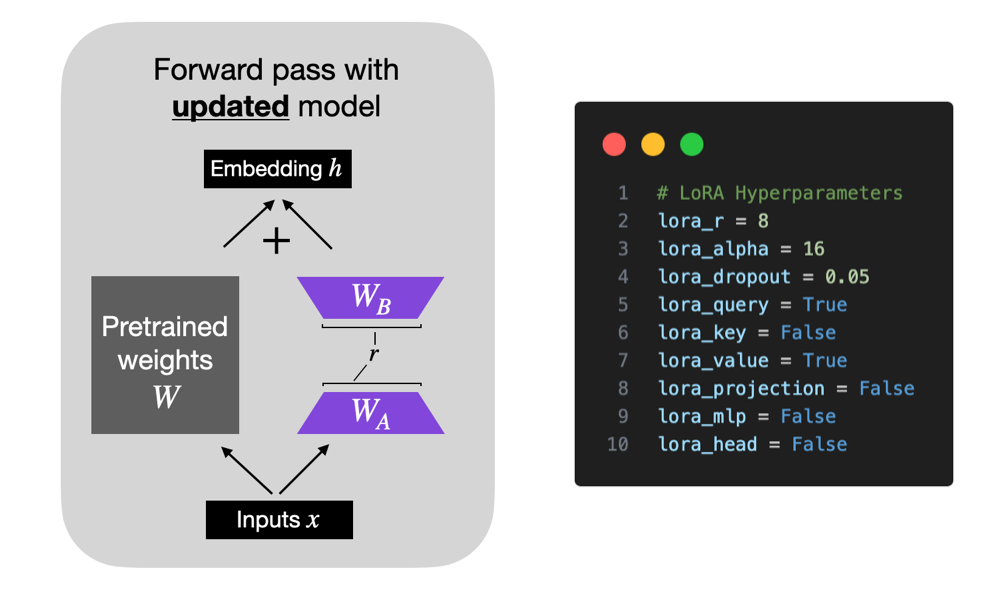
Among the strategies under the PeFT umbrella, LoRA exemplifies how effectively tuning approximately 1% of the parameters can achieve results comparable to full fine-tuning. This significant reduction in resource requirements is the key benefit of PeFT strategies like LoRA, and sets the stage for QLoRA, our main focus.

Now back to QLoRA

Breaking it down, the fundamental concepts behind QLoRA include:

• Quantization

• Dequantization

• Blockwise Quantization

• Double Quantization

• 4-Bit NF4 Precision

• Paged Optimizers

Now we will go through each of these concepts, in an intuitive manner.

Quantization

Quantization reduces a model's size by lowering the precision of its weights and activations, converting them from high-precision formats (like 32-bit floating-point) to lower-precision ones (such as 16, 8, or 4-bit). This process is key for decreasing storage demands, making models less GPU-intensive.

Consider a basic scenario: a model's weights are in 32-bit floating-point, normalized between -1 and 1. To quantize to 4-bit integers (INT4), which represent 16 values from -8 to 7, each weight is mapped to one of 16 buckets within the -1 to 1 range, reducing precision but saving significant memory.

As seen in the diagram, Quantization inherently introduces loss due to rounding values into discrete bins, resulting in Quantization error related to bin size.

Now here’s the magic! Dequantization maps these binned values back to a standard precision, using the bin centers as reference points, effectively transitioning from lower to higher precision.

Quantization and Dequantization: The Math Simplified

Blockwise Quantization

Now transitioning from the vast space of 2³² FP32 values to just 16 in INT4 entails significant information loss. Blockwise Quantization addresses this by adding granularity: rather than applying a broad quantization across the entire -1 to 1 range, it segments the data into smaller, independently quantized blocks, reducing overall quantization error.

With blockwise quantization, as depicted in the diagram, quantization error decreases. Yet, this approach introduces a unique quantization constant for each block (e.g. QC₁, QC₂, QC₃).

Double Quantization

Double Quantization involves quantizing the Quantization Constants themselves. For instance in our previous example these were QC₁, QC₂, QC₃. Pretty meta, I know. While these constants originally exist in FP32 format, they too can be quantized to further optimize storage.

4-Bit Normal Float Precision

NF4 Precision is a specialized data type for quantizing neural network weights, aimed at minimizing memory usage and quantization error. Unlike the uniform distribution of INT4's 16 buckets, NF4 adopts a normal distribution, concentrating more buckets around 0 where weights commonly cluster. This strategy increases precision where it's most needed and uses larger intervals for less common outlier values. Notably, the spacing between NF4's bucket centers is tighter near 0, reflecting the dense weight distribution, and expands towards -1 and 1, effectively balancing precision with storage efficiency.

For example the centers of NF4 datatype are as follows:

[-1.0, -0.6961928009986877, -0.5250730514526367, -0.39491748809814453, -0.28444138169288635, -0.18477343022823334, -0.09105003625154495, 0.0, 0.07958029955625534, 0.16093020141124725, 0.24611230194568634, 0.33791524171829224, 0.44070982933044434, 0.5626170039176941, 0.7229568362236023, 1.0]

You can notice the gaps between NF4's central values are notably smaller around 0 and become larger as they approach -1 and 1.

Paged Optimizers

Paged Optimizers tackle the issue of GPU memory spikes, which frequently occur during training phases and can trigger Out-of-Memory (OOM) errors, often due to variably-sized data batches.

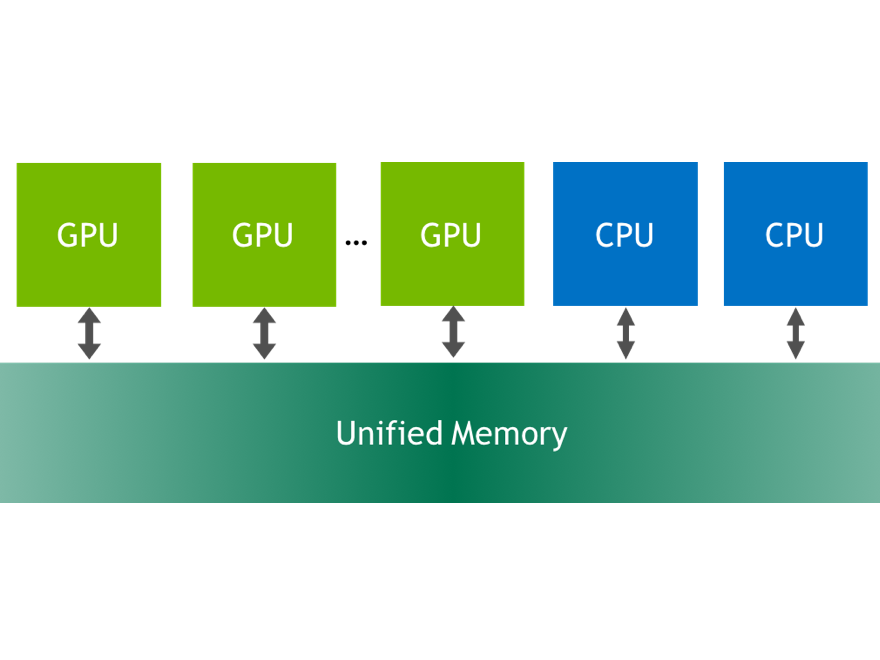
By temporarily transferring the optimizer's state (e.g., Adam) from the GPU to the CPU memory while data is being processed, they effectively mitigate these spikes.

Once the data is ready, the state is moved back to the GPU for continued training. This process leverages NVIDIA's unified memory architecture for seamless page-to-page data transfers between CPU and GPU.

Putting it All Together

1. Quantize model weights (Setup)

   • Normalization - Model weights are first normalized (zero mean and unit variance) this ensure weights are distributed around 0.

   • Quantization - NF4 Blockwise Quantization is applied to all model weights except the ~1% of weights identified by LoRA for training.

   • Double Quantization - Quantization constants are also further quantized

2. Dequantization (Training/Inference)

   • During forward and backward passes all the model weights (except for LoRA adapter weights which keep their original precision) are dequantized back to full precision. Remember weights are stored in memory in their 4-bit quantized form, and just dequantized during computations

3. Paged Optimizers (Optional)

   • If enabled, Paged Optimizers tackle GPU spikes by transferring optimizers state between GPU and CPU as described above

Sources: